通过一道例题理解动态规划

室长收录于找工作就像相亲

2023-02-20 约 1300 字预计阅读 3 分钟

警告

本文最后更新于 2023-02-20，文中内容可能已过时。

例题

给定：一无序数组

要求：找出其中最长的递增的子序列的长度。

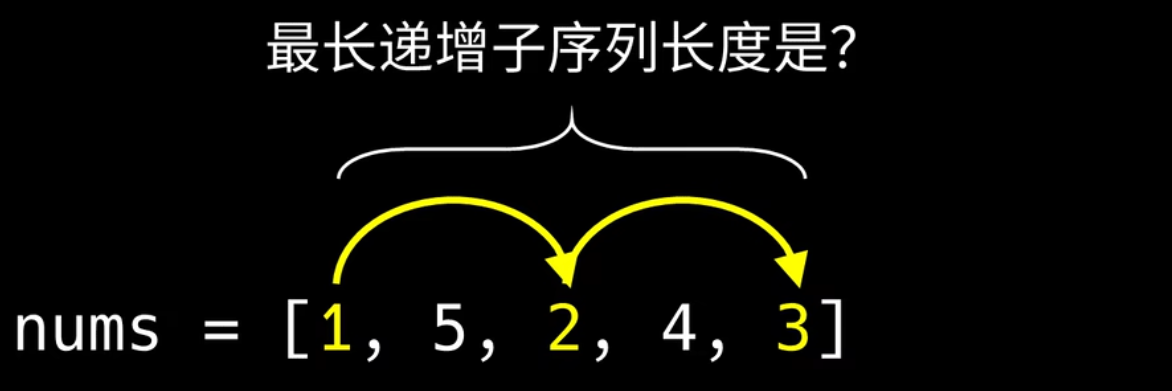
比如给定数组nums=[1,5,2,4,3]，那么其中的1,2,4就算是一个递增子序列，1,2,3是另外一个答案

/leetcode/dp/1.png

暴力枚举法

解题思路

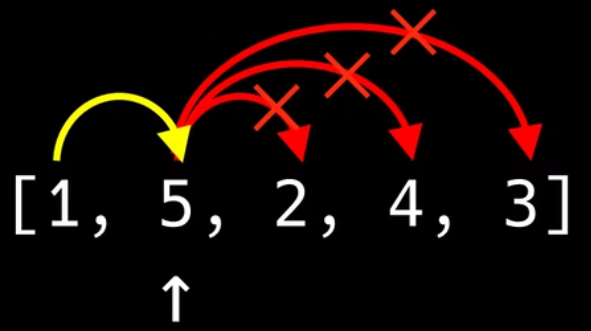
用一个指针遍历数组
如果指针指向的元素的值 > 当前子序列中的元素的最大值，则将该元素加入子序列。

/leetcode/dp/2.png

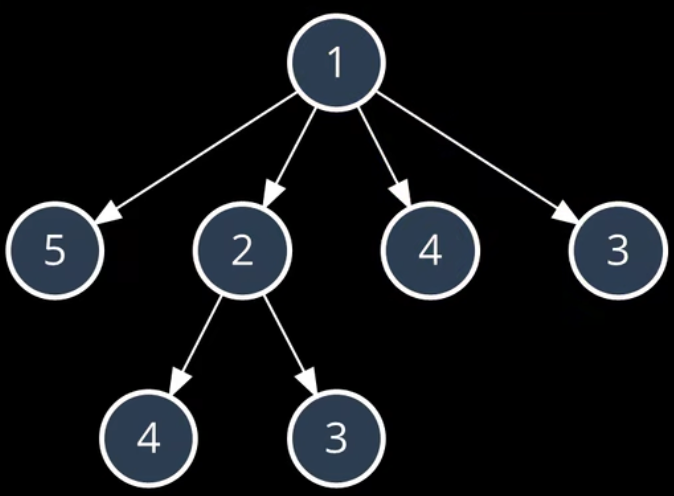
最终会得到这样一个子序列树，相应的，树的层数即为从nums[0]开始最长的子序列长度。

/leetcode/dp/3.png

后面以此类推，得到从nums[1]、nums[2]...nums[n]开始最长的子序列长度，其中的最大值即为题解。

/leetcode/dp/4.png

代码实现

实现一个numsMaxLenWithIndex函数，计算从nums[i]开始最长的子序列长度。
循环调用numsMaxLenWithIndex函数，最终计算出题解。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


def numsMaxLenWithIndex(nums, i):
    if i == len(nums) - 1:
        return 1

    maxLen = 0
    for j in range(i+1, len(nums)):
        if nums[j] > nums[i]:
            maxLen = max(maxLen, numsMaxLenWithIndex(nums, j)+1)

    return maxLen

def numsMaxLen(nums):
    return max(numsMaxLenWithIndex(nums, i) for i in range(len(nums)))

nums = [1, 5, 2, 4, 3]
print(numsMaxLen(nums))

暴力枚举法的缺陷

暴力枚举法的时间复杂度过高：

假设数组长度为 n，意味着有 n 种序列。
一个长度为 n 的序列，每一位都有属于/不属于递增序列这两种情况，一共有 $2^n$ 种情况。

故暴力枚举法的时间复杂度为O($n*2^n$)，这是一个非常缓慢的算法。

动态规划算法

暴力法效率低的根本原因在于大量的重复计算。

比如我们在遍历1,2,4子序列时，已经计算出4作为第一个元素时子序列的最大长度。而暴力法在遍历1,4,x这个子序列时，又重复计算了一遍。

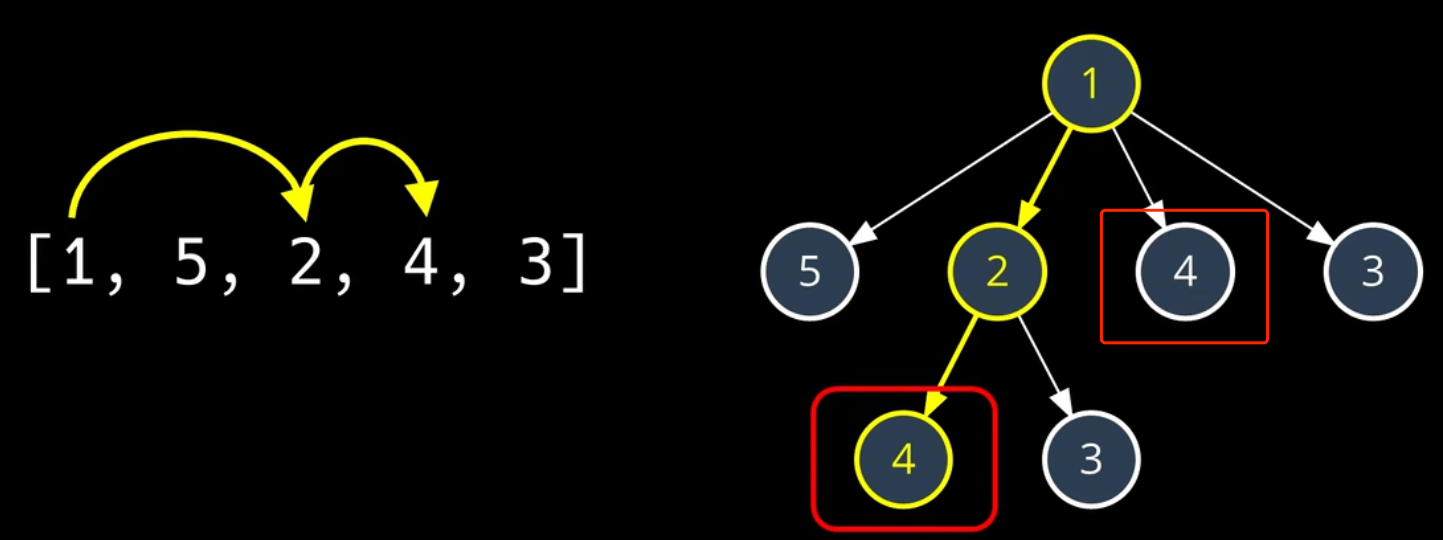
/leetcode/dp/5.png

如果我们在第一次计算的时候，找一个数据结构把计算结果缓存起来呢？

对于这个题而言，我们用一个map来缓存计算结果，记录下"从nums[i]开始最长的子序列长度"

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


indexManLenMap = {}
def numsMaxLenWithIndex2(nums, i):
    # 命中缓存直接 return
    if i in indexManLenMap:
        return indexManLenMap[i]

    if i == len(nums) - 1:
        return 1

    maxLen = 0
    for j in range(i+1, len(nums)):
        if nums[j] > nums[i]:
            maxLen = max(maxLen, numsMaxLenWithIndex(nums, j)+1)

    indexManLenMap[i] = maxLen
    return maxLen

通过避免重复计算来加速整个计算过程，这就是动态规划的核心思想。因为这个特点，动态规划也被称之为记忆化搜索、带备忘录的递归、递归树的剪枝。

话说回来，当前这个解法的时间复杂度是多少呢？这种递归实现还真不好计算出复杂度，所以下一步尝试改成非递归实现。

非递归/迭代实现

通过归纳我们可以发现，如果将从nums[i]开始最长的子序列长度记作L，那么我们可以得到这样一组等式：

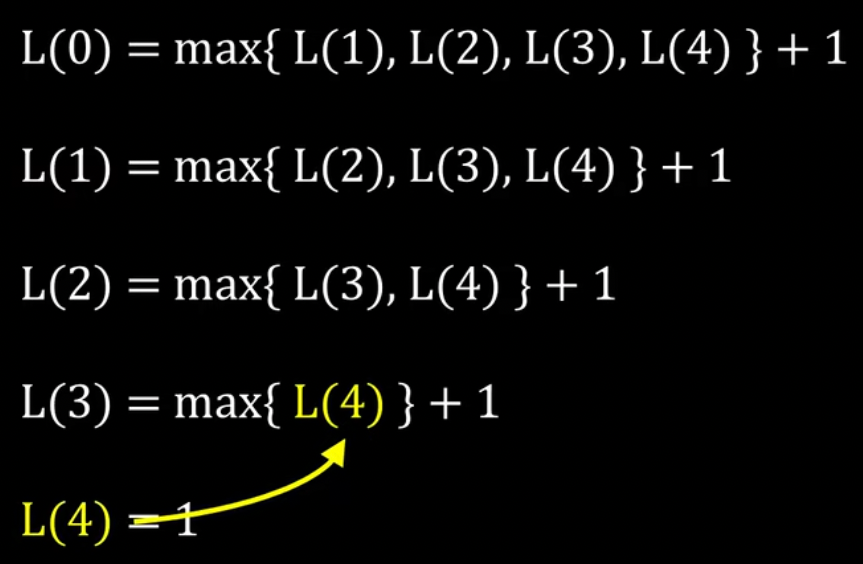
/leetcode/dp/6.png

如果我们倒着开始计算，计算结果恰好可以被下次计算重复利用，从而巧妙地避免了重复计算，代码实现如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


def numsMaxLen2(nums):
    n = len(nums)
    # 初始化
    L = [1]*n

    for i in reversed(range(n)):
        for j in range(i+1, n):
            if nums[j] > nums[i]:
                L[i] = max(L[i], L[j]+1)

    return max(L)

动态规划解题的一般思路

采用暴力法将题目demo的所有答案穷举出来，并画出递归树，尝试写一个递归函数来求解。
如果发现遍历过程中有大量重复计算，可以找一个数据结构将计算结果缓存下来。
最后，我们可以将计算的过程写成表达式，观察公式求解的顺序，尝试改写成迭代形式。

虽然嘴上说起来简单，但是实际上动态规划问题的难度上限极高，难就难在不同问题的迭代表达式的归纳求解往往是天壤之别，没有固定思路，只能靠经验和拼凑。

参考：

https://www.bilibili.com/video/BV1AB4y1w7eT/?spm_id_from=333.880.my_history.page.click&vd_source=3d31fd121c3928864de98496b4f27802

Buy me a coffee~

赞赏

支付宝

微信